複雑系（complex system）

月は狂気を呼び起こす、というのは本当だろうか。月の引力が直接脳に影響を及ぼすとは思えない。こう考えるとき、月と脳は切り離された単純な要素に還元されている。
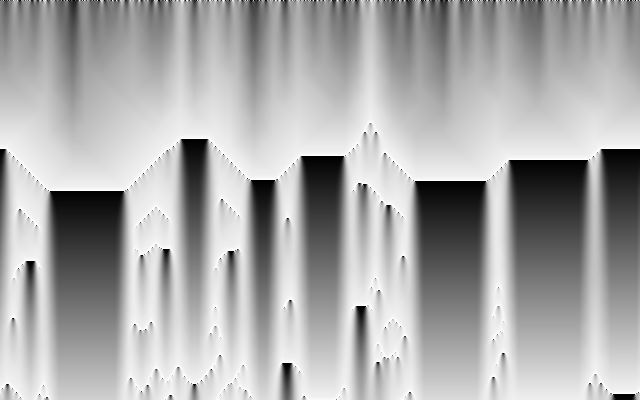
ワペラの個々の細胞の振る舞いは単純だが、ワペラ全体を見渡すと、個々の単純さからは思いもよらない複雑なパターンがあらわれる。ばらばらに見える要素同士が、大きなパターンの中で関連していたりする。このような複雑性を、かつての科学は扱うことができなかった。
複雑系は、単純な要素へとばらばらに分けていく世界観では扱えないような、相互作用するシステムの挙動をとらえようとする領域だ。

散逸構造（dissipative structure）

味噌汁が冷える過程で、味噌が上空から見る雲のように見えることがある。エネルギーが散逸してでたらめが増す過程で、逆に秩序化する「散逸構造」が生じるためだ。
フライパンに味噌汁を入れ、安定したパターンを作ろうと試行錯誤した。熱を表面からうまく逃がし、冷えたかたまりが底に落ちるとパターンが出来はじめる。底の熱分布を均質に保つことで、ベナール対流によるきれいなロール構造が現われる。

自己組織化（self-organization）

指揮者や監督が、全体の設計を行うような制作プロセスをトップダウンという。
それに対して、トップに誰もいないが、勝手にパターンが作られていくことをボトムアップという。巨大なアリ塚に設計者はいない。
ワペラは、複雑系科学ではセルオートマトンと呼ばれるシステムだ。セルオートマトンが面白いのは、精緻で複雑なパターンを無数に隠し持っているのに、それに見合うだけの複雑な設計図がどこにもないことだ。これは驚くべきことだ。

１３人の大工　『オートポイエーシス』（マトゥラーナ＋ヴァレラ）より

初期値鋭敏性（sensitivity to initial conditions）

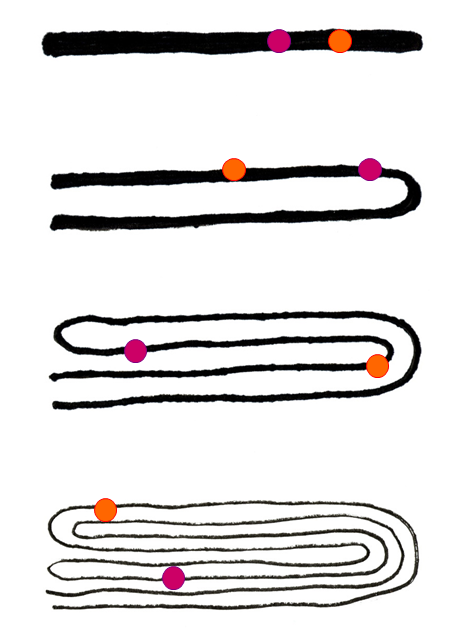
パイ生地を練るとき、練りこまれた豆つぶはどんどん位置の変換にさらされ、はじめの位置がほんの少し違うだけで大きな結果の違いになっていく。これを「初期状態への鋭敏な依存性（Sensitive Dependence of Initial Conditions）」「初期値鋭敏性」などという。このような経過をたどるシステムは、砲弾がどこに落ちるかを計算するようなショートカットでは簡単に予測できない。ステップを踏んで計算してみるしかない。

カオス（chaos）

「思いついた数からはじめよう」といってワペラはスタートしたけれど、これを初期状態という。もし初期状態が、ひとつのセルだけ違ったらどうなる？
何も変わらないこともある。
劇的に未来を変えてしまうこともある。
地球の裏側で蝶がはばたくと、台風が起こるかもしれない。これをバタフライ効果（butterfly effect）という。
ワペラを体験したみんなは、ワペラが規則に従った変化しかしていないのを体験的に知っているが、ワペラの変化はときにはでたらめだったり、パターンらしきものがあったり、単純だったりして、予測ができない。このようなシステムの性質を「カオス」という。

赤い三角形の領域は、ひとつの初期値の違いがもたらした変化。

アトラクター（attractor）

セルオートマトンは、ある時点の状態を、推移規則にそって、次の時点の状態に書き換える循環だ。ワペラのはじめに試したいくつかの規則について、内部状態の変化を追ってみると、順次くりかえされる軌道が見えてくる。

シンクロニシティ（synchronicity）ってある？

電気通信のない時代に、遠く離れた出来事を「虫の知らせ」が伝えてくれたり、その人のことを考えていたらばったり駅で会ったりすることがある。因果の波及速度の限界（光速と言おう）を超えて、共振する事象がある。複数の事象が、因果では説明できない関連をもつことをシンクロニシティという。
シンクロニシティをセルオートマトンでイメージしてみる。ここで光速は45°の斜線で、それよりも横に寝た斜線パターンは光速よりも速い。この同時多発イベントは、近傍の前歴に用意されている。

カオスの縁（edge of chaos）

セルオートマトンは、０か１の状態をもつ細胞のあつまりとして研究されてきた。
ウォルフラムは、その単純なセルオートマトンの分類を試みた。

クラス４は、秩序（クラス１，２）からカオス（クラス３）に至るぎりぎりの境界＝カオスの縁にあらわれる。クラス４は「チューリングの万能計算機」になりうるという。

遍歴アトラクター（itinerant attractor）

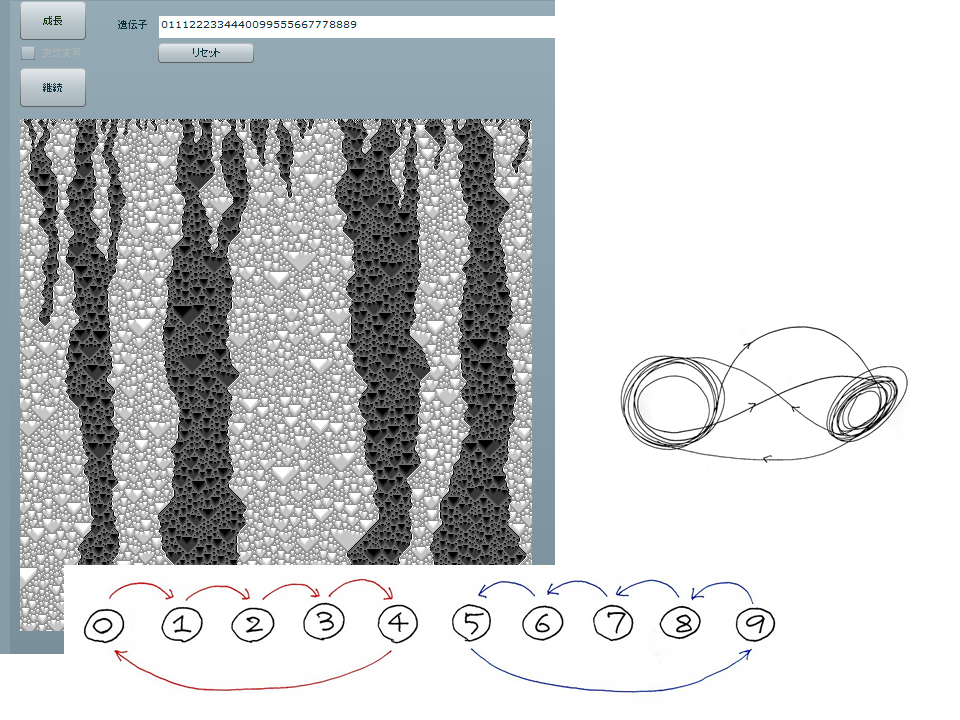
ワペラの地図は、領土を塗り分けるようにいくつかのパターンが入り組むことがある。
ワペラが「カオス的遍歴」と呼ばれる現象をとらえているからだ。
流行の地理的時間的分布、歴史地理空間におけるイデオロギー対立、流血鬼と新人類、脳のデフォルトモード、気まぐれ、などなどさまざまな現象がカオス的遍歴とかかわっている。

ふたたびワペラの内部へ

ワペラの冊子をめくった体験を思い出しながら、ふたたびストリートビューのように、ワペラの地図の内部に入ってみる。

ある遍歴アトラクタの領土の中（たとえば上の白っぽい領域）にいるとき、細胞たちはそこで使われているコードの部分と、状態分布しか見えない。そして突然、別のアトラクタの中（たとえば上の黒っぽい部分）にのみこまれる。

ストリートビューからすると、青天の霹靂のように、ある領土の内部から次の領土の内部に放り込まれることになる。これはとんでもない事件だ。

しかしこれを俯瞰すると、まるで次の領土が用意されていたかのようで、自分がそこでなにをしてもしなくても、いずれは自然にその変化はおとずれることがわかる。ほかにも同じような変化のパターンがあるからだ。もし世界をやりなおしても、どこかに知的生命は生まれ、いずれはコンピュータを作るんじゃないか、という自然過程の力動がイメージできる。

一方で、ワペラ遺伝子の中には千載一遇のような特別のパターンを潜在させているものがある（例は、いま準備しています）。たまたまみつけたかすかなきっかけが、その後の人類をある領土に連れていってくれるような発明、芸術作品がある。そのような事件は、この特別なパターンだろう。

ワペラは、千回のうち９９９回そうなる潜在性と、千回のうち１回しかそうならない潜在性の、いずれをも表現する。内部の視点からは、それらの違いがわからない。

拡張ワペラ

課題：もしワペラコードを、ワペラのセル自身が変更する機構をもっていたら、どんなことが起こるか考えてみよう。

作品

セルオートマトンによる西陣織の柄生成 / Toshihiro ANZAI 1984

mirror mirror / Toshihiro ANZAI 1987

参考

『イオロスの弦―自己組織系の音楽』安斎 1986

『セルオートマトンを彫る』安斎 1986

『コアウォーズの詩人たち』安斎 1987