安斎利洋

１

私の卓上コンピューターに、ある日美しい虫が棲みついた。虫はメモリーという培養器を気儘に食い荒らし、ついには美しい翅をディスプレイに広げるに至った。

プログラマーは虫という比喩を好んで用いるが、虫そのものを好んでいるわけではない。私と虫の出会いもその例に洩れず、私は当所、ほんの思い違いから生まれてしまった虫を退治するのに躍起になっていた。その後、虫が美しい姿を誇示するようになってからは、私の中で虫というメタファーも翅を広げはじめた。虫は遺伝子をもち、組織をもち、五分の魂をもっているように感じられた。

私は今、その虫をセルオートマトンという自己組織系のモデルとして考えることができる。しかし、完成された虫の構造もさることながら、その発生過程において虫はいくつかの示唆を残している。その頃私は、コンピューターの中にピアノやギターの弦を模倣するシステムを作りあげようと企んでいた。

弦はバネで連結された多数の鋼球（質点系）である。それぞれの鋼球は変位と速度のレジスタをもち、隣り合う鋼球との相対的な位置関係によって自らの速度を更新していく。弦をはじくということは、このダイナミツクなシステムに初期状態を与えるということに相当する。たとえば空気抵抗や胴の共鳴など、様々なパラメータを設定することによって、この架空の弦は多様な、そしてアコースティックな娠動を聴かせてくれるはすだった。

はずだった、というのは、この企みが、かの虫の出現によって中座したままになっているからだ。森の中で出会ったあでやかな蛾に足を竦めるように、虫は我を忘れさせるのに充分な美しさをもっていた。その日から私は、アルゴリズムに耳を澄ますのをやめ、ひたすら目を見張ることになる。

プログラマーに忌み鎌われる多くの虫がそうであるように、虫はちょっとした短気といらだちの虚を衝いて登場した。架空の弦はともすると数百分の一ヘルツといった気の長い振勧をするばかりであった（よりリアルな音を望めば、さらに遅くなる）。演算結果を蓄積してほんの数秒の音に圧縮するにしても、何回もの演算が必要になるはずだ。

そこで私は、鋼球の状態を示す数値を範囲の限られた整数に限定して演算速度を上げようと試みた。その上、隣接する鋼球との位置関係から加速度を求める演算をその都度行なっていたのをとりやめ、あらかじめ考え得るすべての場合について演算を済ませておき、それをメモリー上の関数表に書き込んだ（これは常套的な方法である）。

その結果、プログラムはリアルな音を失い、その代償として満足のいくスピードを得た。いや実はこのとき、思いもよらない新しい概念がアルゴリズムの中にすべり込んできたことに、私は気付かなかった。

現実の弦の振動に比べると、蝕まれた弦は実にぎこちない動き方を展開する。以上述べてきたような経緯の中で、私は連続した現実を見るのに三つの不連続のフィルターを挿入してしまった。ひとつは連続した弦を格子点上の質点に寸断してしまったこと、もうひとつは連続した時間を分断してしまったこと、最後は連続した実数を有限の整数にしてしまったこと。そして、連続的な弦を決定的に離散的システムに化けさせたのは関数表である。もはやここでは、１という数値はＡであっても”木”という記号であってもいいのである。かくして虫が棲息する土壌ができた。私にとって弦の模倣はもうどうでもいいことに過ぎなかった。弦のいたるところに生ずる予期せぬ歪が、まるで生きた物のように繁殖する萌しを見せた。私はまだぎこちない動き方しかできない虫を培養するために鋼球（これからはむしろ細胞と呼ぶべきである）の状態を記憶する変数をひとつに簡略化した。細胞のとり得る状態もほんの16段階にしてしまった。固定されていた弦の両端は自由にし、しかもそれぞれを連結してしまった。ついでに隣接する細砲の状態から次にとるべき自らの状態を定める関数表を、ほとんど子供の悪戯のようにでたらめに書き替えた。fig.1 はそうしたアルゴリズムの出したテクスチャーである。

fig.1

texture、textile、textと、同根の語をたどるアナロジーでこのパターンを見ることができる。横糸は弦であり、縦糸は音色（時間）である。また、横糸は直線上に等間隔で並んだ細胞であり、縦糸は細胞の成長パターンである。これを縦横に編まれたtextと見るなら、パラグマチックな横糸とシンタグマチックな縦糸を見ることができよう。有限の状態からある状態を選択している細胞は、一意的なシンタックスによって縦糸を塗り分けていくに過ぎない。にもかかわらず、縦糸は横糸と響き合いながら、単純ではない展開を見せている。個々の細胞の協調によって多様な文脈を形成する。視点をさらに引いて全体を眺めると、我々はカオスの中にある法則性を感ずることができる。めくるめく変化の中にある部分が全体を組織するのは、パロールがラングを担う構造に対比することもできるだろう。このアルゴリズムをそっくりそのまま言語の雛形とするのは無理があるが、少なくとも複雑さと単純さ、多様性と一様性を同時に孕む構造を生成するのに、記号が世界を分節化するような恣意性と不連続性は少なからす作用しているようである。

その後私は、恣意的な関数表を遺伝子に見立て、これを書き替えることによって、より美しいパターンを生成するという工芸的な作業に没頭した。いくつかの遺伝子は、ランダムに与えた初期状態をまたたく間に安定した単調さの中へ引き込んでしまった。またあるものは、長い間初期状態の分布を記憶し続けた。巧みに作られたあるものは、安定した繰り返しのなかにある複数の領域が熾烈な境界争いを繰り広げ、まったく予期できない歴史を展開して見せた。いずれも、初期状態の乱数を別に選べばまったく異なるパターンを生成する。しかし、いずれも同一の遺伝子からは遺伝子に特有の構造を見ることができる。

局所的な相互作用が大域的に複雑な構造を形づくる様は、生態系のゆらぎを思わせるものがある。またでたらめな初期状態を固有の構造の中に消化していく様は、生命が物質を核酸の文字列によって構築するのにも似ている。複雑なパターンを生成する遺伝子は、細胞の列がゆくゆくどのような姿に成長するかに関する記述をもっているわけではない。にもかかわらず、細胞によって塗り分けられたテクスチャーを組織するのは、ごく単純な機能を有する細胞自身である。

２

このようにある機能を有する無数の自動機械（オートマトン）を規則的に並べたモデルは、私のコンピューターだけに忽然と出現したわけではない。実はそのコンピューターそのもののモデルを考えたフォン.ノイマンが、1950年代に生物の自己増殖を模倣する機械を作るために二次元セルオートマトン（細胞自動機械）を導入している。セルオートマトンは、有限の状態をもつ同ーのセルを幾何学的に整然と配列した構造をもっている。それぞれのセルは、近傍のセルの状態だけを知ることができる。それらの状態から、セルは次の時刻に自分がとるべき状態を決定する。私の「虫喰った弦」は、セルが直線上に等間隔で並んだ一次元セルオートマトンであるということができる。
ノイマンは自己増殖モデルを作るにあたって、はじめは現実の生物が空間を動き回るように、散在する部品を捕獲しては自分自身のコピーを再構成するようなモデルを考えていた。その後、いくつかの状態をとり得るセルを格子状に敷きつめた一様セル空間を想定し、状態の分布の推移が同じ分布を作り出す自己増殖機械を考えはじめたといわれる。前者に比べると後者はより記号的な自由を獲得している。斉一なセル構造のなかでは、自己増殖機械は機能を連れて動き回る必要がない。水面を伝播する波のように、状態の分布だけがここでは意昧を持っている。かくしてセルオートマトンの概念が定式化された。★１

Ｓ.ウォルフラムは最近の研究で、非常に簡略な一次元セルオートマトンの繰り広げる変化を、実験的な方法で追跡している。ウォルフラムにとってコンピューター内のオートマトンは、実験室で電子の挙動を追跡するのと同様に実験対象である。たとえば我々は、弾丸の軌跡を追う以前にその落ちる場所を知ることができる。我々は単純な系においては実際にやってみる以前に解を求める近道を知っているからである。しかし単純な要素が集積してある複雑さをもったとき、我々はもはや近道をもたない。たとえば乱流の成長を、実験的な方法によらずに正確に予測することはできない。こうした簡約化できないシステムは、実際に追跡する以外に近付く手立てがない。★２

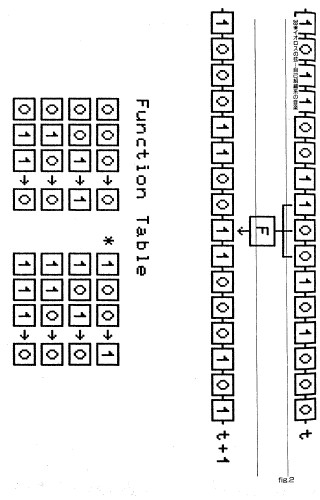
ウォルフラムは、０と１のふたつの状態しかもたない一次元セルオートンに様々な初期状態を与え、どのような歴史を展開するか追跡することによってセルオートマンを大きく４つに分類している。第１のタイプはすべてのセルが０か１の単一の状態に落ち着いてしまう。第２のタイプは初期状態によって、１と０が棲み分けながら安定するか、周期的なくりかえしパターンに安定する。第３のタイプは生成と消滅のカオス的なパターンを生成する。最も複雑な第４のタイプは、パターンが拡大縮小しながらまったく予想のつかない展開を示す（fig.2）
このように分類されたセルオートマトンのいくつかは、自然界の連続的システムと同じように、系をある特定の状態に引き付ける吸引（アトラクタ）を想定することによって説明することができる。第１のタイプは、系がある単一の状態に引き付けられている。第２のタイプは複数の吸引をもっているが、初期状態によってそれはすぐに結着がつき、安定した分布や規則的な繰り返しのなかに落ち着こうとする。第３のタイプはそれほど簡単ではない。同様に複数の状態に引き付けられているが、吸引自体が互いに入り組ん複雑な構造をもっている。乱流を引き起こすストレンジ・アラクタがこれにあたる（フラクタル溝造をもったこの奇妙な吸引は、最近コンビュータ・グフィックスの表現を通して視覚的に把握することができるようになった）。

第４のタイプ、はセルオートマトンにまったく別なアスペクトを開いてくれる。それは、このタイプがチューリング機械に匹敵する万能コンピューターになるのではないか、という予想である。万能コンピューターはあらゆる計算可能な問題を解くことができる。逆にある問題を解く万能コンビュータが存在しなければ、その問題は本質的に解決不可能である。万能コンピューターはそういう概念装置である。
今、私の卓上コンピューターがあるプログラムを実行している。その結果があらかじめ別の方法で予測できるなら、私はすぐさま実行を中断するキーを押すだろう。また、もっと簡単に結果を得るアルゴリズムを知っているなら、同様に実行を中断してプログラムを書き替えるだろう。同等の機能をもつコンピューターの振舞は、同等の機能をもつコンピューターによってしか追跡できない。つまり本質的に簡約化できない。第４のタイプが作り出すパターンもまた同様に簡約不可能である。つまり自分自身の最も簡約な記述は、自分自身なのである。

複雑なパターンを生成するセルオートマトンの振舞は、オートマトンの単純な機能に集約することはできない。初期状態が設定され、あらかじめ定められた規則によって一意的に推移するというまったく決定論的なシステムであるにもかかわらず、我々はその行方をあらかじめ知ることができないのである。世界はそうしたシステムに満ちている。このことは生命現象の分子レヴェルでの解明が、人間の精神構造の解明にまで飛躍することは決してあり得ないことも暗示している。

試みにこういう実験をしてみると面白い。ある複雑な挙動を示すセルオートマトンに適当な初期状態を与え成長させる。それを再び初期状態に引き戻し、そのなかのたった一つのセルの状態をわずかに変える。その後成長するパターンに現われる莫大な影響は驚嘆に値する（fig.3）。

fig.3

こうした自己組織系では、個は全体の行方を担っている。つまり、全体を記述するためにはどの部分を欠くこともできないのである。
充実した組織は、それ以上濃縮された表現をもたない。これは、我々が詩について考えるときも頭をかすめる。私は、自然界の物理的なシステムに限らず、自然言語といった高度に複雑化した記号的システムにおいても、その潜在的な表現能力の原理をここに読み取ることができるような気がしている。
言説は言うまでもなく語の選択過程である。しかし我々は決して一意的に定められた関数によって言葉を選んでいるわけではない。統辞法は、次に来るべき言葉をある部分集合に拘束するシステムである。つまり言説は、一つの要素を選択すると同時に系全体を方向づけるという二重の選択過程である。
このような不確定要素を孕んだシステムを、ただちにオートマトンのモデルと結びつけることはできない。しかし、ウォルフラムの観察はここでもいくつかの有効な説明を可能にしてくれる。

fig.4

fig.5

たとえば日常の言語は２番目のタイプを連想させる（fig.4）。相互作用がある範囲から伝播しないセルオートマトンの挙動は予想が可能である。たとえば周期ｎの繰り返しに陥ったセルの状態は、時刻（mod n）によって予想することができる。同じように、相互作用の範囲が限定された日常の言語は、一意的に意昧に辿り着くことができる。
それに対し詩的言語は、３、４番目のタイプを連想させる（fig.5）。ここではある話線（discourse）の切断面にあらわれる選択可能な言葉の集合が、表にあらわれた話線の前歴からただちに定められない。それは、詩的言語が顕在的な一本の話線ではなく、潜在的な近傍の話線と響き合った全体だからである。
我々はそういう多旋律のテクスチャーのなかに、意昧の拡張を見出す。時に我々は日常的な推移規則から逸脱した主旋律によって、思わぬ副旋律の作用を暗示される。隠喩とはそうした近傍の話線との相互作用である。
詩的言語はこうして、言語に自己組織系としての有機的な全体を恢復する。そういえば、言語を最初にセル空間に照らして語ったのはＦ.ソシユールである。もちろんソシュールは二次元セル構造などと言うべくもなく、そのモデルを”チェス”と呼んでいる。★４
ひとたび定跡から逸脱した試合の行方は、棋譜をたどる以外にそのすべてを示す手立てがない。私のディスプレイに描き出された「虫喰った弦」のパターンもまた、自然界の複雑なテクスチャーと同様、それ以上濃縮できない緊密さにおいて美しいのである。

３

もはや「虫喰った弦」は私の個人的所産ではない。しかしあくまで私の個人的（パーソナル）コンピューターから発生した虫は、私が培養し続けなくてはならない。私は最近、音に端を発している虫を再び音の世界へ帰してやれないかと考えている。そう考えているうちに、ひょっとすると西洋古典音楽の歴史は、弦に巣喰った虫の成長と死の過程ではないかと思い始めている。
西洋音楽のシステムは、他のどの系に属する音楽よりも過激な離散化から出発している。連続的な混沌のなかにあった音は、記譜法や平均律の発明によって分断された記号的システムのふるいにかけられる。演奏における摂動、偶発的な変伯、任意の選択を捨象することによって、作曲という行為はいきなり鏡舌になったと思われる。演奏と切断された音楽はあり得ないが、演奏を切断せずには西洋音楽史は成立し得なかった。西洋音楽は、出発に際してまずそういう装置を用意するところから構築されている。
我々はたとえば、協和音に調和を感ずるのは生得的であると考えがちである。それ以前に、完全５度の周渡数レシオは物理的に裏付けられていると考える。しかしこれらは、ソシュールがラングというシステムを生得的な言語能力であるランガージユと区別したように、音楽の構造とは切り離されるべきものである。音楽は作られたシステムである。つまり、我々の脳のどこを探っても、生理的に裏付けられた音楽の構造などどこにもない。
調性もまた作られたものである。古典的な和声学はある終状態への過程として築かれ、我々の耳もそれを希求するかのように感ずるが、それはあらかじめシステムが内蔵している吸引を聴いているのである。調性は再帰的に組織された「奇妙なアトラタ」であると考えることもできよう。我々の耳は作品という一つの系の中で、複雑な力学によって連れ去られようとしながら、選ばれた音に連れ戻される過程を経験する。作曲家にしてみれば、それは自律的な自己組織系との弁証法的な戦いである。作曲家は音を選択するにあたって、掻き消されそうな遠方からのアトラクタを聴き分け、それによってまったく新しいアトクタを開拓する。これを再び先に述べた言語との比較にあてはめれば、それは詩的言語の生過程と酷似するはずだ。
和声学は言語における統辞法と同様、次に来ることが可能な要素をある部分集合に拘束する。しかしそれは浸蝕し難い推移規則として君臨し続けたわけではない。音は、作品、同時代、音楽史という階層的な系全体と響き合いながら系全体の可能性を問い続ける。その結果、西洋音楽は用意された記譜法、作曲と演奏の分離、平均律といった装置そのもののあり方を聞い直すところまで来ている。

私は今、煙草の紫煙が美しい乱流を形成するのを見ている。目を上方に移すと、そこには統計的に均質な、かたちの無い煙が立ち籠めている。西洋伝統音楽はまさしくそのような無形への路を辿った。それは、あらかじめ用意された終状態であるかもしれない。あるいは、より大きな渦が再び乱流を形づくる兆であるかもしれない。
そういう文脈を踏まえて、私の「虫喰った弦」を奏でる方法がないかというのが、私の当面するテーマである。このシンプルなモデルをなるべく複雑化せずに、それによって音を組織し、音楽として構築する方法を深さなくてはならない。
この作業はcomposeというより音楽装置のdesignと呼ぶのがふさわしい。セルの状態としていくつの変数を割り当てるか、どのような近傍をもったどのようなセル空間を作るのか、それらを音のパラメータにどう割り付けるか、そしてどのような推移規則をプログラムするか、こうした決定の総体は、和声学のシステムに比肩し得る情報量をもつかもしれない。
残念ながら私は、まだまとまった成果を得てはいない。しかし、ごく単純なモデルによってでも、その単純さからは思いもよらない組織を作り出すことができる。たとえばウォルフラムが３番目に分類した振舞をするセルオートマトンであるなら、局所的な調和と大域的なカオスが飛躍もなく繋がり、どこを切り取っても同じ印象をもちながら同じになることがないような組織が展開する。しかもその成長は、プログラムを中断しない限り終りがない。いわばこれは、我々を取り巻く環境をシミュレートしている。

最終的に私が思い描いているのは、調性、モード、リズム、そして音色まで自律的に自己組織化する装置である。もちろんそれは、私自身の選択を常に反映できるようなシステムにしたいと考えている。私自身が一個の自己組織系として、愛すべき虫の仲間入りをするわけである。

fig.1 「虫喰った弦」一次元セルオートマトンの描き出したダイアグラム。横軸はセル空間、縦軸は時間である。16状態、近傍は左右それぞれ１つと自分自身の3つである。それぞれのセルは、近傍の状態を加算し、推移関数表から次の時刻の状態を求めている。この関数によって、描き出されるパターンは多様である。初期状態は乱数を用いた。プログラムは文献5を参照されたい。

fig.2 ウォルフラムが観察したセルオートマトンの4つのタイプ。タイプ１～３は次のようなものである。いま１次元の格子点にセルが下図のように並んでいる。

━ C(i-2) ━ C(i-1) ━ C(i) ━ C(i+1) ━ C(i+21) ━

それぞれのセルは0か1の2状態をとりうる。それぞれのセルは、次の時刻にとる状態を、隣接するセルの状態によって決定する。すなわち、

C(i,t+1) = F( C(i-1,t), C(i,t), C(i+1,t) )

Fは推移関数である。これを表であらわすと、タイプ1に例示したものは次の通りである。

C(i,t+1) 0 0 0 0 0 1 0 1
C(i-1,t) 0 1 0 1 0 1 0 1
C(i,t) 0 0 1 1 0 0 1 1
C(i+1,t) 0 0 0 0 1 1 1 1

C(i,t+1)の値を下から並べた２進数10100000は10進では160である。これを160番と呼びなら、タイプ２、３に例示したものは、それぞれ108番と18番である。

タイプ4は5つの近傍をもつ。すなわち、
C(i, t+1) = F( C(i-2,t), C(i-1,t), C(i,t), C(i+1,t), C(i+2,t) )
ウォルフラムは５つの近傍の合計によって決まるようなFについて観察している。タイプ4に例示したものは、合計が2と4のときに1。それ以外は０という規則である。

fig.3 乱流のようなカオス的挙動をみせるセルオートマトンは、わずかな摂動によってまったく異なる歴史を展開する。2つのパターンは、初期状態（最上列）の中央の1つが異なるだけである。影響が伝播していくのがわかる。

fig.4 局所的には複雑な振舞をみせているが、大域的にはウォルフラムが2番目に分類したものに属する。

fig.5 3番目の分類に属する。横方向の繋がりが密接である。

参考文献

1)ノイマン「自己増殖オートマトンの理論」1960 高橋秀俊訳岩波書店

2)ウォルフラム「科学と数学のソフトウェア」サイエンス 1984/11 日経サイエンス社

3)特集「オートマトン構造」数理科学 1985/7 サイエンス社

4)ソシュール「一般言語学講義」1916 小林英夫訳　岩波書店

5)安斎利洋「パーソナル・コンピュータ・グラフィックス」1986 美術出版社