美術家は時折、いかさま博徒があざやかに骰子を操るように、偶然を美事に手なずけてしまうことがある。たとえば円空の振るう刃は、薪割りの刃よりあざやかに、木の節理に潜む自然の表情を開示しようとする。あるいはマックス・エルンストが、絵具を挟んだ二枚の紙を引き剥がすと（décalcomanie）、そこには宇宙樹の相似形態が浮かびあがる。

美術家がいかに素材の物性を知悉したとしても、素材のふるまいはあくまで予見できない〈偶然〉である。その気ままなふるまいを、美術家は〈必然〉的な意志によって、ある内的なビジョンに近づけていこうとする。とりあえず、私はそう考えておくことにする。しかしこの考えは、すぐさまリバーシブルのコートのように裏返すことができる。〈必然〉的なのは自然の過程であり、想像力はあたかも〈偶然〉のように、自然の間断なき作用を縫ってどこへでもかすめ抜けていこうとする、というふうにである。どうやらここで、〈偶然〉と〈必然〉という二元論はまったく効力をもたないようだ。

コンピュータのディスプレイを前にした現代の円空たちにとって、素材－コンピュータ・グラフィックスにおける〈偶然〉と〈必然〉はごく自明のことのように思われる。 ＣＧ作家が、木に刃を振るうようにプログラムにパラメータを与えると、プログラムは〈必然〉的に計算過程を展開しはじめるだろう。そこには原理的に、寸分の〈偶然〉も入る余地がない。もしそこに〈偶然〉を挟み込みたければ、たとえば乱数発生ルーチンを呼べばいいのである。すっかり馴染み深くなった「フラクタルの山脈」は、ある初期形態を再帰的に崩していくことによって描かれるが、ここで我々は、乱数表という自明な〈偶然〉が、プログラムという自明な〈必然〉に取り込まれていく様を見ることができる。

しかしながら我々をとりまく自然において、〈偶然〉と〈必然〉はそれほど自明に分離できない。現実の山は「乱数表」をもっているわけではないし、全体から部分へと形づくる図面を持っているわけでもない。自然はむしろ、全体の中での自分の役割などまったく関知しない〈部分〉が、有機的に関係することによって〈全体〉を形づくっている。自然は、個々のエレメントの局所的な働きから全体の挙動をすぐさま予見させないような、ある飛躍を孕んでいる。そうしたシステムにおいて、〈偶然〉と〈必然〉は表裏をなす対概念ではなく、同一面上の連続した概念である。個々の要素はまったく決定論的にふるまっているにもかかわらず、それらの協力によって作られる全体はカオス的である場合もある。あるいは、まったくでたらめに分布する要素の集合が、あたかも目的をもつかのように、ある秩序に引き込まれる場合もある。

こうした現象をうまくとらえるモデルに、セルオートマトンがある。コンピュータの中に作られたセルオートマトンは、まるでその向こうに自然を隠し持っているように、〈偶然〉や〈必然〉では語り尽せない節理を見せてくれる。私は、思わずそれを彫りたいという衝動にかられる。

セルオートマトンの基本的な発想は、極端なまでに離散的に作られたそのシステムに見ることができる。まず空間は格子点上のセルに離散化されている。それぞれのセルは、近傍のセルとの関係で、次の時刻にいっせいに状態を更新する。ここで時間も連続を断たれる。しかもたいていの場合、セルは有限の状態（だとえばＯと１）しかとらない。

セル空間の構造や状態数によって、セルオートマトンはどのようにでも複雑化していくことができる。しかし基本的に、セルオートマトンはごく単純に設計されることが多い。我々を驚かせるのは、ごく単純でまったく決定的なシステムが、確率的な過程としてしかとらえられないような多様なふるまいを見せることである。

写真ａｂは、１次元格子点に「細胞」を並べた、16状態のセルオートマトンの成長過程である。各セルは、次の時刻の状態を３つの近傍の関数によって決定し、それを下方向に順々に描いている。ａとｂは、同一の初期状態（最上列）から出発している。いずれもまったく決定的な機能によって遷移しているにもかかわらず、我々はその行方を予測することができない。

これとは別な関数をもったあるセルオートマトンは、すべてのセルをひとつの終状態に吸引してしまう。そういった性質は、推移関数を「プログラム」することによって操ることができる。ある状態に吸引される過程に罠を仕掛けて別な周期に引き込んだり、さらに別な吸引を仕掛けたり、そうしたプログラム上のテクニックを弄することによって、我々は大域的な性質をコントロールできる。つまり我々は彫刻家が木を選定するように、セルオートマトンを設計することができる。しかし我々は、その木にどんな節理が畳み込まれているか、プログラムを実行するまで知ることができないのである。

私はこのアルゴリズムを用いて、コンピュータ・グラフィックスに風変わりなひとつのジャンルが形づくれるような気がしている。水彩絵具のにじみや、油絵具のマチエールと同じ次元で考えれば、セルオートマトン絵画は現代の円空やエルンストたちの想像力を大いに刺激するはずだ。

写真ｃは、６つの近傍をもつ２次元のセルオートマトンによって、乱数で作られた砂地のような初期分布を成長させた、ある時刻の分布パターンである。私は、あらかじめこのプログラムに推移関数テーブルを書き込んだという以外、ここに至る成長過程に何ら手を下していない。つまりこれは無垢の素材である。しかし、このセルオートマトンは都合の良いことに、初期状態の影響を残しながら棲み分けていく傾向を持っている。これは造形素材としては、手なずけやすい性質をもった例である。

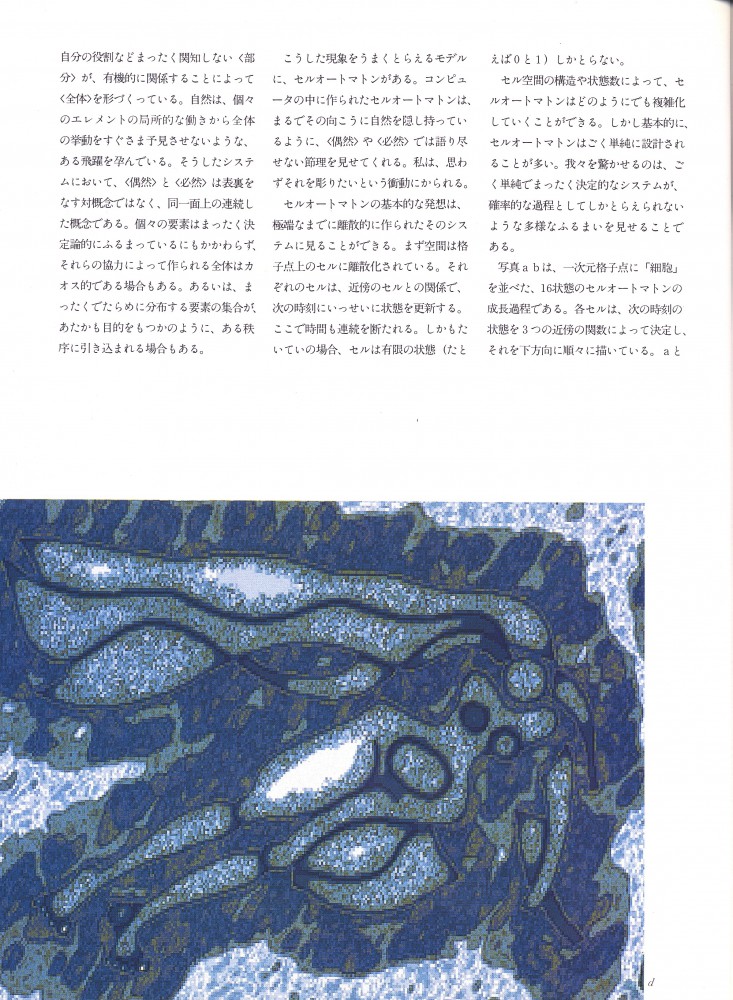
もしこのようにして生成される分布パターンに不満があれば、私はその一部を無理矢理書き替えることもできる。あるいは空間、時間の場によってセルオートマトンの機能に偏りをもたせることもできる。これはいわば、乱流を堰くしがらみを立てるようなものである。私は間接的に、ディスプレイに塗られたセルオートマトン顔料をこねくりまわすことができるのである。写真ｄは、そのようにして作られたテクスチュアをコラージュした作品である。

美術家にとって素材は、たんにある形態を実現するための媒体であるばかりでなく、自律的な無数の過程を可能性として畳み込まれた装置であると言うことができよう。円空にとって木は、無数の節理が畳み込まれたオートマトンの塊である。すると、セルオートマトンによる造形という発想はそれ程奇抜なものではないことがわかる。素材を巧みに手なずけた造形作家というのは、いわば自然という巨大な並列処理計算機のオペレーターであるとも言えるからである。